[算法]搜索-散列表(hash表)

哈希表

哈希表在时间和空间上做出权衡，在很多情况下是简单符号表的最佳选择。
如果我们不受时间限制，可以用顺序查找的方式查找一个无序的数组，以降低空间成本，如果我们不考虑空间，将键值完全散列，以键值作为数组的索引，我们就能达到O（1）的访问速度。我们通过改变哈希表的参数来在空间和时间上做出取舍。

前面学习到的几种算法比如红黑树，二叉搜索树，查找插入时间复杂度最快也只能到O(logn)，散列表查找插入时间复杂度达到常数级别，但是需要牺牲一定的计算索引的时间。

将键转化为数组的索引，不同的数据类型需要相应的散列函数

正整数的散列函数通常用除留余数法。选一个素数作为除数，将键值作为被除数，将余数作为散列值。

字符串也可以用这种方式。我们将字符串当作一个大整数。

int hash = 0;
for(int i=0;i<s.length();i++){
	hash = (s[i]+ R*hash)%M;
}

将字符串的每一个字符的unicode加上R的i次方再相加，利用除留余数法获得哈希值。

哈希表存储的是键值对，其查找的时间复杂度与元素数量多少无关，哈希表在查找元素时是通过计算哈希码值来定位元素的位置从而直接访问元素的，因此，哈希表查找的时间复杂度为O（1）。

哈希冲突是指不同的键值有相同的散列值，也就是处理两个或多个三劣质相同的情况，如果我们将哈希值作为一个数据的唯一标记的话（应用如校验文件完整性等），我们应选用更复杂的哈希函数避免哈希冲突（如sha-256等），但是在在符号表的应用里，我门需要冲突来权衡时间和空间复杂度。

处理哈希冲突主要的两种方法：

大小为M的数组中的每个元素指向一条链表，链表中的元素就是相同哈希值的元素。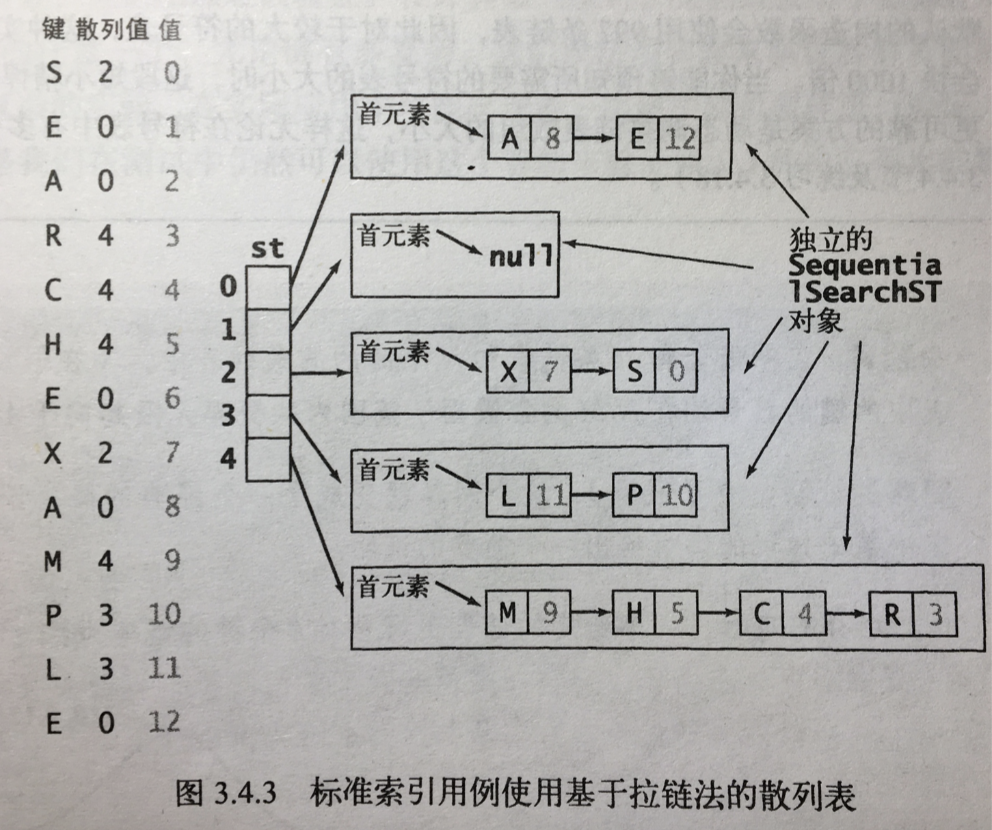

查找分为两步：首先根据散列值找到对应的链表，然后在链表上顺序查找相应的键。

链表的平均长度： N/M

实现基于拉链表的散列表，目标是选择适当的数组大小M，使得既不会因为空链表而浪费内存空间，也不会因为链表太而在查找上浪费太多时间。装填因子>=1

使用数组中的空位来解决冲突，用大小为M的数组保存N个键值对，M>N，他属于开放寻址法。当碰撞发生时，我们直接检查散列表的下一个位置。但是这种方法容易出现聚集，影响效率。

为了避免聚集，我们还有二次探测法，地址增量不是1，而是1^2,2^2,3^2,4^2…，但是不能探测到哈希表上的所有储存单元。

装填因子 = （哈希表中的记录数） / （哈希表的长度），及哈希表被装填的概率，线性探索法要求的装填因子比较小.

在查找时，我们查找某一个键的值，先将键经过hash函数获得哈希值，根据哈希值找到对应的数组位置，有可能直接命中，若未命中则继续下一个位置查找，直至命中或遇到空值表示查找失败。

** 由于空值代表查找失败，所以我们在删除一个元素的时候不能简单的将元素置空，而是添加一个钙元素已经被删除的标记，以避免影响接下来的查找。

无序查找

插入数据时需要和元素做对比，如果存在就不插入，存在则插入==>O(N)
查询时需要一个个对比数据==>O(N)

有序查找

查找过程是折半，对比的次数最大是log(N+1) ==>O(logN)

但是插入的过程需要将插入的值后边的值往后挪，查找要插入的元素是否存在需要lgN，往后挪元素平均N/2 ==>O(lgN +N/2)

所以二分查找适合静态表，也就是不允许添加元素的表的查找

有序查找

插值查找是二分查找的改进，比如我们要找1-1000中的987，从500开始查找显然不如900开始查找的性能高，插值查找就是改善了二分查找(1/2)的折半，而是自适应，计算mid的函数：mid=low+(key-a[low])/(a[high]-a[low])*(high-low)

插值查找适合分布比较均匀的数据。

有序查找

查找平均O(lgN),失衡最坏O(N)

插入时间类似于二分查找，但是由于是链表实现不需要挪动后边元素==>O（lgN）

有序查找

查找 O(lgN)

插入 O(lgN)

无序查找

单纯论查找复杂度：查找复杂度为O(1)（注意，在查找之前我们需要构建相应的Hash表）